acwing_3422_左儿子右兄弟

题目描述

对于一棵多叉树，我们可以通过 “左孩子右兄弟” 表示法，将其转化成一棵二叉树。

如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。

换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。

给定一棵包含 个结点的多叉树，结点从 至 编号，其中 号结点是根，每个结点的父结点的编号比自己的编号小。

请你计算其通过 “左孩子右兄弟” 表示法转化成的二叉树，高度最高是多少。

注：只有根结点这一个结点的树高度为 。

例如如下的多叉树：

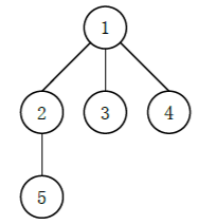
可能有以下 种 (这里只列出 种，并不是全部) 不同的 “左孩子右兄弟”表示：

其中最后一种高度最高，为 。

输入格式

输入的第一行包含一个整数 。

以下 行，每行包含一个整数，依次表示 至 号结点的父结点编号。

输出格式

输出一个整数表示答案。

数据范围

对于 的评测用例，；
对于所有评测用例，。

输入样例：

1
2
3
4
5

5
1
1
1
2

输出样例：

1

4

什么是左儿子右兄弟

首先，对于这样一棵多叉树，每个节点连接的有子节点，兄弟节点，父节点。

例如，1号节点有2 3 4三个子节点，这三个节点在构造二叉树时就被放在左边，这就是左儿子。

2号节点有3 4两个兄弟节点，所以在构造时，这两个节点都放在了右边，这就是右兄弟。

因为 第一个 与 父节点 连接的兄弟节点有三个，所以说有三种以上可能。这样子研究起来肯定很复杂。我们换个角度，把这些二叉树看成是一个一个链表。

链式前向星

来个大点的图，将其改为二叉树，其中一种方案是这样的

运用链式前向星的思想，每个节点创建一个单链表，链表存储的是父节点与子节点。1 是根节点，2 3 4 5是子节点，被放在该链表内。可以看到我用虚线隔开的三个区域，中间的区域就包含着2 3 4 5，6 7是2的子节点，8是4的子节点。从上图应该能够看出一点规律来：兄弟节点被排成了一列。

这可以说是一个有趣的性质，启发我们使用链式前向星存图。

递归与贪心

如何求得最大长度？获取每个节点子树高度。上图中1的子节点中谁的子树高度最高？是2。

我们如何求子树的最大高度？遍历

遍历1的子节点，对于1的每个子节点，要求它们的子树高度，就要遍历它们的子节点，直到到底，才一级一级返回他的子树高度。这就类似于一个递归的过程。

那兄弟节点之间的顺序呢？开头说到多个兄弟节点会有多种排法，既然我们都求出了拥有最大的子树高度的节点，那在给他加点高度，也就是放到最下面，那岂不是锦上添花。所以不用考虑过多，只要把子树高度最高的加上兄弟节点数就好

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

#include<iostream>
#include<cstring>
using namespace std;

const int N = 100010;

struct{
	int v, nxt;
}e[N];

int n, idx, h[N], u;

void add(int a, int b)
{//链式前向星存点
	e[++idx].v = b;
	e[idx].nxt = h[a];
	h[a] = idx;
}

int dfs(int now)
{
	int maxn = 0, cnt = 0;
	for(int i = h[now]; ~i; i = e[i].nxt)
	{
		int j = e[i].v;
		maxn = max(maxn, dfs(j));
		cnt ++;
	}
	return cnt + maxn;
}

int main()
{
	memset(h, -1, sizeof(h));
	cin >> n;
	for(int i = 2; i <= n; i ++)
	{
		cin >> u;
		add(u, i);
	}
	cout << dfs(1) << endl;

	return 0;
}