正睿-1139-序列

正睿-1139-序列

题目描述

小 D 正在研究序列。

对于一个正整数序列而言，小 D 认为他是好的，当且仅当任意相邻两个数字均为 一个奇数和一个偶数。

形式化地，对于一个序列 b1, b2, · · · , bm 而言，小 D 认为他是好的，当且仅当对 于任意 1 ≤ i < m，有 bi 为奇数且 bi+1 为偶数，或 bi 为偶数且 bi+1 为奇数。

小 D 得到了一个长度为 n 的序列 a1, a2, · · · , an，小 D 想要通过重新排列它，使 它变为一个好的序列。 小 D 定义一种重新排列方案的代价为重排后每个数字位置差的绝对值之和。小 D 想要最小化重排的代价。

此外，小 D 还想在最小化重排代价的基础上，最小化结果序列的字典序。 但是小 D 并不会，请你帮帮他。

注： 我们称一个序列 c1, c2, · · · , cn 字典序小于 d1, d2, · · · , dn，当且仅当存在一个介 于 [1, n] 之间的 i，使得 ci < di，且对于任意 1 ≤ j < i，有 cj = dj。

输入

从标准输入读入数据。 第一行一个正整数 n 表示序列的长度。

第二行 n 个空格隔开的正整数，表示 a1, a2, · · · , an。

输出

向标准输出输出答案。 输出一行 n 个空格隔开的正整数，表现字典序最小的结果序列。 数据保证一定可以得到至少一个好的序列。

样例

输入

5

5 3 1 4 2

输出

5 2 1 4 3

约定

1 <= n <= 100000

1 <= ai <= 1000000000

分析

看到这题面完全没有想法（除了暴力

然后就思考2分钟，题解两小时

题解的想法：将 奇数偶数相隔性、 字典序最小 和 最小代价 三个条件分开想。

首先要知道一个性质：如果奇数多于偶数，那肯定是奇数包着偶数，例如：1 4 3 2 5。这个时候奇数必须在奇数（下标）的位置上。而当偶数多于奇数，奇数就在偶数下标上。

还是举个例子好理解：假如有两个奇数位置空缺 3 7。而现在有两个符合条件的数 1 3 分别在 4 6 的位置上。

这是最优的情况

好

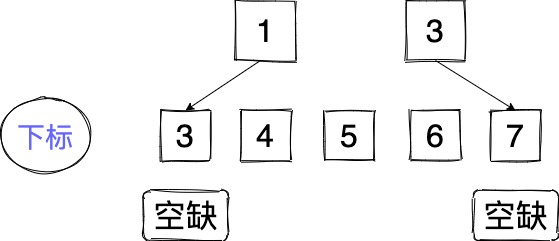
不好的情况

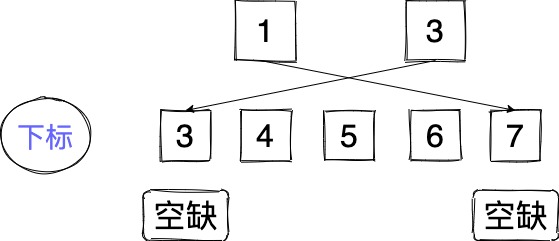
So, …… 显然吧

也就是如果一个向左一个向右时，左边的向左。

而都要向左或向右时都一样。

向左向右都有的话，我们可以遍历两遍数组，正反各一次。

开一个优先队列。把数字向左放时，反着遍历，要尽量把小一点的数向前放没问题；那么向右时，要正着遍历， 怎么让小的往前放？取负数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
#include<iostream>
#include<vector>
#include<cstdio>
#include<algorithm>
#include<queue>

using namespace std;

#define ll long long
#define N 100010
#define re register

int n, a[N], t[3], ans[N], anss[N];
int num;
priority_queue<pair<int,int> > ss;

ll query(int s, int t, int *aa)
{
    ll ans1 = 0;
    while(!ss.empty())
        ss.pop();//清空
    int s1 = 0, t1 = 0;
    for(int i = 1; i <= n; i ++)
    {
        if(a[i] % 2 == s)
            s1 ++;
        if(s1 > t1)
        {
            if(a[i] % 2 == s)
                ss.push(make_pair(- a[i], i));
            if(i % 2 == t)
            {
                aa[i] = - ss.top().first;
                ans1 += i - ss.top().second;
                ss.pop();
            }
        }
            if(i % 2 == t)
                t1 ++;
    }
    while(!ss.empty())
        ss.pop();
    s1 = 0, t1 = 0;
    for(int i = n; i >= 1; i --)
    {
        if(a[i] % 2 == s)
            s1 ++;
        if(s1 > t1)
        {
            if(a[i] % 2 == s)
                ss.push(make_pair(a[i], i));
            if(i % 2 == t)
            {
                aa[i] = ss.top().first;
                ans1 += ss.top().second - i;
                ss.pop();
            }
        }
            if(i % 2 == t)
                t1 ++;
    }
    return ans1;
}


int main()
{
    scanf("%d", &n);
    for(re int i = 1; i <= n; i ++)
    {
        scanf("%d", &a[i]);
        t[a[i] & 1] ++;
    }
    if(t[1] != t[0])
    {
        if(t[1] > t[0])
        {
            query(0, 0, ans);
            query(1, 1, ans);//当奇数多于偶数，奇数对应奇数位，偶数对应偶数位
            for(int i = 1; i <= n; i ++)
                printf("%d ", ans[i]);
        }
        else
        {
            query(0, 1, ans);
            query(1, 0, ans);//与上面的相反，奇对偶，偶对奇
            for(int i = 1; i <= n; i ++)
                printf("%d ", ans[i]);
        }
    }
    else//奇等于偶时有两种情况
    {
        ll st1 = query(0, 0, ans) + query(1, 1, ans);
        ll st2 = query(0, 1, anss) + query(1, 0, anss);
        if(st1 > st2)
        {
            for(int i = 1; i <= n; i ++)
                printf("%d ", anss[i]);
        }
            
        else if(st2 > st1)
        {
            for(int i = 1; i <= n; i ++)
                printf("%d ", ans[i]);
        }
        else
        {
            for(int i = 1; i <= n; i ++)//判断字典序
            {
                if(anss[i] != ans[i])
                {
                    if(anss[i] > ans[i])
                        for(int i = 1; i <= n; i ++)
                            printf("%d ", ans[i]);
     
                    else
                        for(int i = 1; i <= n; i ++)
                            printf("%d ", anss[i]);
                    break;
                }
            }
        }            
    }

    return 0;
}